Fundamentals to clustering 3D point cloud data
Why is unsupervised segmentation the key to sustainable automation? Automation in point cloud data processing is central for building efficient decision-making systems and to cut labour costs. The identification of objects of interest in these massive datasets constitutes the basis of many applications. While new supervised deep-learning architectures show promising results, the amount of available labelled 3D data is often insufficient for a good generalization. This is where unsupervised approaches and clustering shine.
What is data clustering?
Clustering algorithms allow data to be partitioned into subgroups, or clusters, in an unsupervised manner. Intuitively, these segments group similar observations together. Clustering algorithms are therefore highly dependent on how one defines this notion of similarity, which is often specific to the field of application.
Clustering algorithms are often used for exploratory data analysis. They also constitute the bulk of the processes in AI classification pipelines to create nicely labeled datasets in an unsupervised/self-learning fashion.
Within the scope of 3D Geodata, clustering algorithms (also defined as unsupervised segmentation) permit to obtain a segment soup that becomes the backbone of several processes such as feature extraction, classification or 3D modeling as illustrated below.
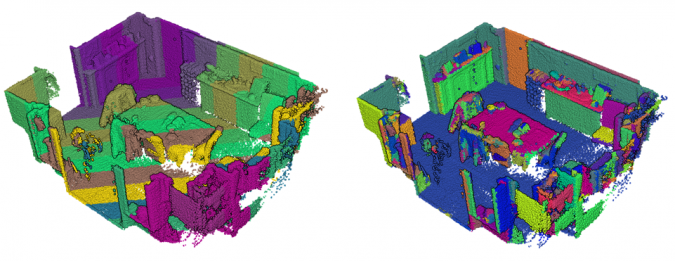
They most often act in addition to a dimensionality reduction algorithm that allows the different attributes (called dimensions) to be viewed in two or three dimensions. If a “view” presents sufficient decorrelation, a clustering algorithm can be used to form sub-groups of these points: the clusters. In this way, the relationships between the points can be visually represented. Alternatively, instead of representing the entire data, only one representative point per cluster can be displayed.
Once clusters have been identified, data can also be viewed using only one representative per cluster and discarding the others.
Why is this useful?
Clustering algorithms are particularly useful in the frequent cases where it is expensive to label data. Take the example of annotating a large point cloud. Annotating each point by what it represents can be a long and tedious job, to the point that the people doing it can unintentionally introduce errors through inattention or fatigue. It is cheaper and perhaps even more efficient to let a clustering algorithm group similar points together and then only involve a human operator when assigning a label to the cluster.
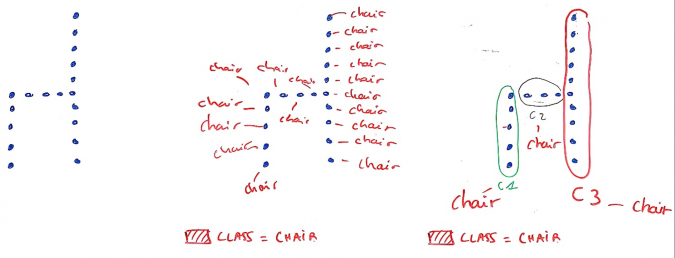
Thus, clustering algorithms can be used to extend a property of one of the points in the same cluster to all the points in the same cluster (in the previous example, the represented chair object.).
We will define several criteria to be optimized to define an interesting partition of the data. These are then used to derive some of the best-known clustering algorithms (K-means, K-NN, Mean-shift…)
How to know if the clustering is representative
In the case of unsupervised algorithms, the purpose of the algorithm is less obvious to define than in the case of supervised algorithms, where there is a clear task to accomplish (E.g. classification or regression). The success of the model is therefore more subjective. The fact that the task is more difficult to define does not prevent a wide range of measures of the performance which I will detail below.
Distances and similarities
Clustering means grouping together the closest or most similar points. The concept of clustering relies heavily on the concepts of distance and similarity.
These concepts will be very useful to formalize:
- (1) How close two observations are to each other;
- (2) How close an observation is to a cluster;
- (3) How close two clusters are to each other.
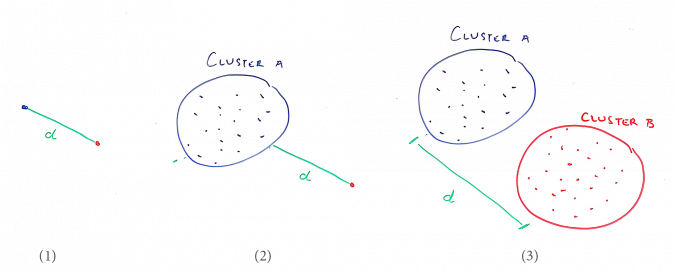
The most commonly used examples of distances are the Euclidean distance, and the Manhattan distance. The Euclidean distance is the “ordinary” straight-line distance between two points in Euclidean space. The Manhattan distance is so-called because it corresponds in two dimensions to the distance traveled by a taxi on the streets of Manhattan, which are all either parallel or perpendicular to each other.
Thus, a distance can be used to define a similarity: the further apart two points are, the less similar they are, and vice versa. For injecting a very tiny bit of math, we can transform a distance d between x and y into a similarity measure. Another common way to define similarity is to use the Pearson correlation which will take into account the shape of the distribution rather than their amplitude, which the Euclidean distance mainly takes into account. The choice of the distance measure is therefore important.
Cluster shape
The shape of a cluster is an important element that we initially describe as:
- (1) Tightened on themselves: two close points must belong to the same cluster
- (2) far from each other: two points that are far apart must belong to different clusters.
Often, we search for clusters tighten on themselves. Let us translate these properties with an example, using the Euclidean distance. First, we can compute the centroid of a cluster (the barycentre of the points of this cluster) pretty easily. The homogeneity of a cluster can then be defined as the average of the distances of each of the points contained in this cluster to the centroid. In this way, a tightened cluster will have a lower heterogeneity than a cluster of scattered points. Then, to characterize not one cluster, but all clusters in our dataset, we can calculate the average of the homogeneity of each cluster.
Secondly, we want the clusters to be far from each other. To quantify this, we usually define the separation of two clusters as the distance between their centroids. Once again, we can calculate the average of these quantities on all the pairs of clusters obtained.
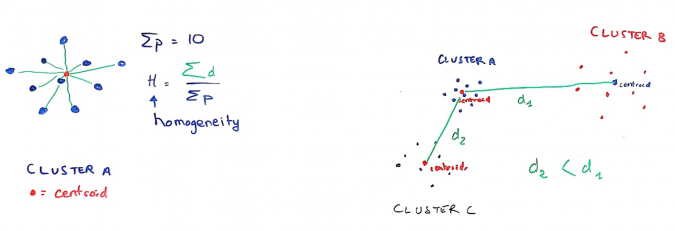
We now have two criteria to optimize: homogeneity and separation. To make it easier for us, we can group them into a single criterion, the Davies-Bouldin index. The idea of this index is to compare intra-cluster distances (homogeneity) — which we want to be low — to inter-cluster distances (separation), which we want to be high. For a given cluster, this index is all the weaker as all the clusters are homogeneous and well separated.
Another way to quantify how well a clustering meets these two requirements (homogeneity and separation) is to measure the so-called silhouette coefficient. To assess whether a point belongs to the “right” cluster. For this, we try and answer (mathematically) two questions:
- Is p close to the points of the cluster to which it belongs?
- Is the point far from the other points?
Cluster stability
Another important criterion is the stability of the clustering: if I run the algorithm several times on the same data with a different initialization, or on different subsets of the data, or on the same slightly noisy data, do I get the same results? This criterion is particularly relevant when choosing the number of clusters: if the number of clusters chosen corresponds to the natural structure of the data, the clustering will be more stable than if it does not.
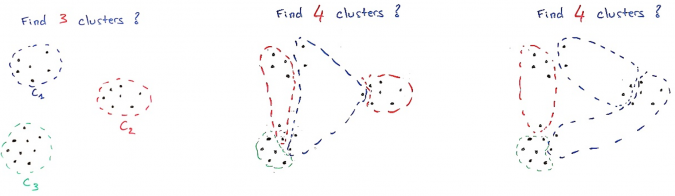
On the example above, an algorithm that tries to determine 3 clusters will reasonably find the three clusters we see. But if it is asked to determine 4 clusters, the distribution in these 4 clusters will be more random and will not necessarily be twice the same. This is one way to determine that 3 is a better number of clusters than 4.
Compatibility with domain-specific knowledge
Very often, we will also evaluate a clustering algorithm “by eye” and see if the proposed clusters make sense. Do the points grouped in this cluster all represent the same object? Do the points in these two clusters represent different objects?
To do this more neatly, we can work on a dataset on which we know a reasonable partition of the data. We will then compare this partition with the one returned by our clustering algorithm. For example, we can work with a point cloud partitioned by planar shapes. The next step is to evaluate whether the groups formed by the clustering algorithm correspond to those defined a priori.

It’s easy! It’s like evaluating a multi-class classification algorithm. But not so fast: if we are interested in whether the same objects belong to the same cluster, it doesn’t matter whether this cluster is the first, the second, or the k-th cluster. Therefore, specific performance metrics must be used to evaluate the concordance of two partitions of the dataset.
An example of these measures is the Rand index (and its more robust Adjusted Rand Index). The Rand index is the proportion of pairs of points that are grouped in the same way in both partitions: either because, in both cases the points belong to the same cluster, or because, in both cases, the points belong to different clusters.
Conclusion
Unsupervised and self-learning methods are very important for solving automation challenges. Particularly, in the era of deep learning, creating labeled datasets manually is tedious, and ways to alleviate this process are more than welcome. Clustering algorithms provide crucial solutions for this, and are used to partition a dataset into sub-groups of similar observations:
- They can be used to better understand the data;
- They can be used to facilitate data visualization;
- They can be used to infer data properties.
Then, to evaluate a clustering algorithm, we can look at:
- the shape of the clusters it produces (are they dense, well separated). The silhouette coefficient is often used here;
- the stability of the algorithm;
- the compatibility of the results with domain-specific knowledge, which can be evaluated using enrichment measures.
References
Poux, F., Billen, R., 2019. Voxel-Based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS Int. J. Geo-Information 8, 213. doi:10.3390/ijgi8050213
Poux, F., Neuville, R., Nys, G.-A., Billen, R., 2018. 3D Point Cloud Semantic Modelling: Integrated Framework for Indoor Spaces and Furniture. Remote Sens. 10, 1412. doi:10.3390/rs10091412
Poux, F., Neuville, R., Van Wersch, L., Nys, G.-A., Billen, R., 2017. 3D Point Clouds in Archaeology: Advances in Acquisition, Processing and Knowledge Integration Applied to Quasi-Planar Objects. Geosciences 7, 96. doi:10.3390/geosciences7040096
Value staying current with geomatics?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories to help you learn, grow, and reach your full potential in your field. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired.
Choose your newsletter(s)