Map Generalisation
Quality Benchmarks Through Optimisation
Decades of research on map generalisation have resulted in an abundance of heuristic algorithms, evaluation of the performance of which is vital for choosing the most suitable for a certain application. Proper evaluation methods are, however, missing. The author proposes an approach based on optimisation methods adopted from the field of operations research.
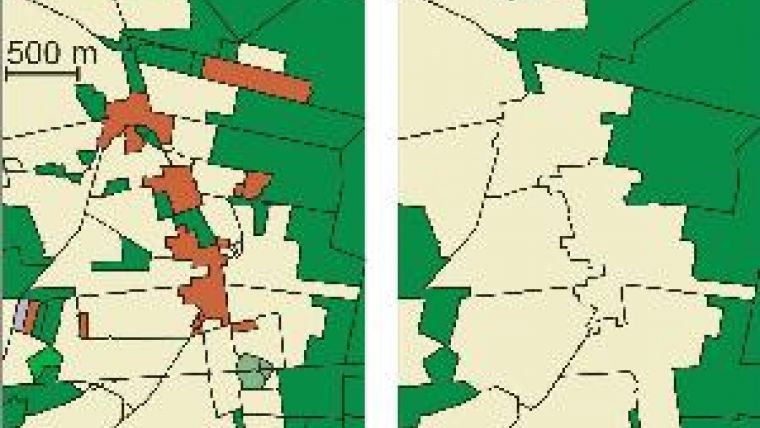
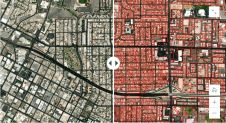
Driving to your holiday destination, you may wonder why the idyllic village along the road is not represented on your map. Is it because a cartographer decided to omit the village to improve map readability? It's more likely today that a computer did the job, as ‘map generalisation', the decision regarding which details to represent at a certain map scale, has become highly automated. The map in Figure 1 (left), for example, shows a village represented by red-brown polygons. The application of generalisation using a region-growing algorithm removes the entire village from the map (Figure 1, right). This happens because the algorithm employs a rule merging all polygons smaller than 0.4 km2 with their most similar neighbour. Is this a good rule? Hard to say, even bearing in mind the criteria by which a good map is made.
Requirements
An obvious way to improve the performance of map generalisation algorithms is to increase their speed. This, however, does not tackle the problem of arriving at satisfactory solutions. Here optimisation approaches from the field of operations research would appear appropriate. Generally these approaches are based on a model comprising a set of requirements to be fulfilled by a solution, and a cost function that is to be minimised. Solutions obtained with this optimisation approach can be used as benchmarks for evaluating the quality of heuristic methods such as the abovementioned region-growing algorithm.
For maps consisting of polygons, national mapping agencies often stipulate that the area of each polygon should exceed a pre-set value; this, like map scale, may depend on the type of object it represents. Indeed, this requirement can be applied in an optimisation approach. Cost function needs to be defined such that it reflects the quality of the generalised map. The measure of quality of the generalised map should reward similarity between the original map and the generalised map and penalise differences. This means that a change in object type of a polygon has to be charged. The cost of such change can be defined according to the area of the polygon. The type of change can also be reflected in function by, for example, penalising change of cropland into grassland less than change of cropland into forest. The cost discrepancy here arises from semantic similarity between cropland and grassland being much greater than between cropland and forest.
Optimisation
The generalisation problem now needs to be expressed in a form readable by a solver. The problem of generalising a polygon map can be formalised as an integer linear program, which comprises a linear objective function and a system of linear inequalities in integer variables. In this form the problem can be solved by, for example, applying the commercial solver CPLEX. An example of a map generalisation solution using this optimisation approach is shown in Figure 2 (left). In this map the area of each generalised polygon is larger than the threshold applied and therefore the object type of just a few small polygons needed modification. So we see that in contrast to the result in Figure 1, the village is still there. But does the map appropriately represent the situation on the ground? The upper part of the village polygon shows a long and narrow annex. Obviously, with cost function applied, the cost of converting the smaller forest (green) polygons into village was less than converting the larger village polygon into forest or cropland.
It is not necessary to study the details of the optimisation algorithm used by the solver in order to understand how it produced such an unsatisfactory result. The solver CPLEX uses an exact algorithm: that is, it guarantees a globally optimal solution and hence can be treated as a black box. One can simply rethink the set of quality criteria and requirements and restart the algorithm with a revised model. To avoid long, elongated polygon parts, the cost function was modified to penalise non-compact polygons. The optimisation algorithm was then restarted, resulting in a map that better reflects the situation on the ground (Figure 2, right). The approach thus allows map generalisation algorithms to be improved in an incremental way.
Benchmarks
As all exact algorithms for solving integer linear programs have in the worst-case scenario exponential running time, they can be too slow for generalising large, detailed maps. Still, these exact algorithms remain valuable, as they can be used to optimally generalise map samples and thus evaluate the performance of heuristic algorithms. The optimisation-based algorithm can be made faster by introducing heuristics that yield satisfying solutions with respect to the quality measures. Assessing the quality of these heuristics can be done by using as benchmarks the optimal results obtained for small samples. For generalising very large maps, a good strategy is to design heuristics that segment the generalisation problem. The resulting smaller instances of problem can be solved independently. Introducing heuristics allows for generalisation of a map sheet in about one hour, while the results are similar to those of the exact algorithm.
Lines and Buildings
We have discussed above the case in which both original and generalised map consist of polygons. Another problem is the generalisation of polygons into line elements. For example, in a large-scale map rivers are represented as polygons; at smaller scales rivers need to be represented by their centre lines. Generalisation can be done by computing the straight skeleton (Figure 3) but whether this can be integrated into an optimisation approach is still an open question.
Can the above optimisation approach be applied to buildings, too? Basically, building simplification can be achieved through reducing the number of points by setting a geometric error tolerance and requirements that ensure a topologically correct map. The result, however, may show loss of shape regularities typical of buildings. To avoid this, measures can be added that favour solutions with right angles while keeping the dominating edge directions of the input polygons (Figure 4). An open problem is the preservation of symmetries in a building polygon.
Concluding Remarks
The biggest advantage of our optimisation approach is that it separates definitions of map requirements and quality from algorithmic solutions. Presumably the development of new automatic map-generalisation algorithms will continue as long as user needs change. This makes the optimisation-based approach promising, in that it allows the generalisation problem to be incrementally modelled.
Further Reading
- Haunert, J.-H., Sester, M., 2008. Area Collapse and Road Centre Lines Based on Straight Skeletons. GeoInformatica, 12(2): pp169-191.
- Haunert, J.-H., Wolff, A., 2010. Optimal and Topologically Safe Simplification of Building Footprints. In: Proc. 18th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM-GIS'10), pp 192-201.
- Haunert, J.-H., Wolff, A., 2010. Area Aggregation in Map Generalisation by Mixed-integer Programming. International Journal of Geographical Information Science, 24(12):
1871-1897.
Value staying current with geomatics?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories to help you learn, grow, and reach your full potential in your field. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired.
Choose your newsletter(s)