Open Data and Quality

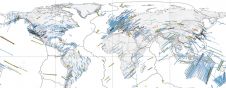
For decades, quality as an essential dimension in using geodata has been neglected by many GIS users. As a result of open data and the tendency to combine geodata from a wide diversity of sources, one now faces the dilemma of discrepancies arising between one dataset and another. In the meantime, many people have burned their fingers and suddenly there it is: after decades of disregard, the quality issue is now appearing high on the agenda of GIS users. Few of them grasp that the subject is not only key, but also complex. To illustrate the scale of the quality challenge, I will focus here on a rather technical topic: measures of precision, in particular CE90, RMSE and σ. I appreciate that these may be unfamiliar terms to many people. CE90 stands for ‘circular error at 90% confidence’. This accuracy standard, developed during WWII by the USA, is a convenient single measure for describing the accuracy of an (ortho)image or a map. It is expressed as the horizontal distance that any point in the image will differ from its actual position on the ground for 90% of the time. To calculate the distance, a set of ground control points (GCPs) is used. The coordinates of the GCPs in the image are measured and subtracted from the actual values as measured in the terrain by an accurate device, e.g. a high-definition GNSS receiver. Graphically this may be interpreted as the radius of a circle, which contains 90% of the residuals (red circle in Figure). Root mean square error (RMSE) and standard deviation (σ), which are other measures of precision, are directly related to CE90. The planar or circular RMSE, obtained by combining the RMSE along the X axis and the RMSE along the Y axis using the Pythagorean theorem, is 0.466 x CE90 (yellow circle in Figure). If positional precision is given as σ, which is usually derived from an RMSE computation and set equal to the RMSE, CE90 and σ can be easily converted. As a rule of thumb, σ gives a two times better impression of precision than CE90. Whatever measure of precision is used, if positional precision is key for the task at hand it is wise to validate the communicated values by measuring accurate GCPs, well distributed over the scene, oneself. This is also to identify possible space dependency of the error distribution which can be analysed and visualised by drawing vector plots.