Parallel Computing in Photogrammetry
Seamless Orthomosaic Creation from Massive Imagery
The race between data production and processing capacity has been going on for many decades, with data production usually on the winning team. This is also true for airborne and space-borne imagery, as the amount of images captured by satellite sensors and aerial cameras is growing not only steadily but also rapidly. How can the abundance of pixels be processed into photogrammetric products quickly and effectively? The answer lies in parallel computing. Today, computer clusters enable fast and affordable processing of photogrammetric tasks. Read on to learn how parallelism speeds up the creation of seamless orthomosaics.
By Andrey Yu. Sechin, Racurs, Russia
Traditionally, software has been written for serial computation. The algorithm is put into operation as a series of instructions which are executed on a central processing unit (CPU), one instruction at a time in succession. Parallel computing – a dominant research area in computer architecture aimed at speeding up computation – is mainly implemented through multi-core processors. The use of multiple CPUs enables many calculations to be conducted simultaneously. As a result, complex computational tasks are broken down into smaller components which can be processed at the same time. Each CPU executes its part of the process simultaneously with and independently of the others. The results are combined afterwards. Photogrammetric processing of massive volumes of images may also benefit from parallel computing. To illustrate the massiveness of the amount of data produced by spatial and airborne sensors, European Pleiades-1А and Pleiades-1B satellites have the capacity to acquire 2,000,000 km2 per day, while the VisionMap A3 Edge aerial camera captures 5,000km2/hour of imagery with a GSD of 20cm.
Seamless Mosaics
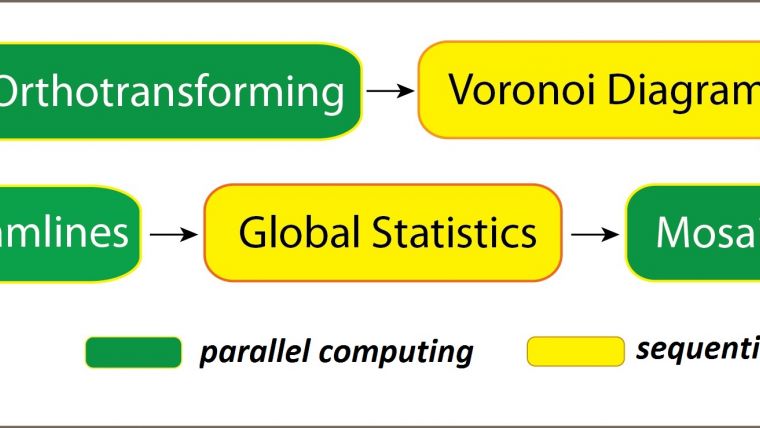
The creation of seamless orthomosaics consists of several steps, including (Figure 1):
- project creation and reading the images from storage devices
- ortho creation of each image using the corresponding digital terrain model (DTM)
- determination of seamlines
- image statistic gathering for brightness adjustment
- seamless orthomosaic computation and storage in separate sheets.
The time taken to download images from a provider of satellite images or from an aerial camera storage unit will be disregarded in the present considerations. Ortho creation of each image, called ‘images orthotransforming’ in Figure 1, can be conducted in parallel. Seamlines are the edges which constitute the outline of the part of the image used for the creation of the orthomosaic. The determination of seamlines consists of two steps. First an initial seamline is created based on simple topological relationships, particularly the Voronoi diagram. This ensures that the nadir part of all images is preferably selected. This step cannot be done in parallel, but it is completed very quickly. Next, each edge of the Voronoi diagram is automatically refined based on the image content so that the edges of the outline curve around buildings and do not cross roads at right angles. This step can be performed in parallel.
Brightness adjustment is mathematically complex and consists of several stages including collection of image statistics, such as brightness histograms, and global brightness adjustment. Global brightness adjustment cannot be conducted in parallel, but the local brightness adjustment can be done per tile and along seamlines, thus through parallel computing. The last step stitches the images together in one mosaic. This process is carried out on a separate CPU.
Test
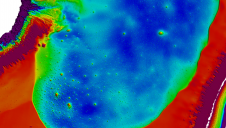
To test the time efficiency of the process developed, the blue, green and red bands of multispectral satellite images were used with a ground sampling distance (GSD) of 1m covering a total area of 37,234 km2 in Khanty-Mansi Autonomous Okrug, Russia. The diverse images were taken during different seasons and under a variety of light conditions (Figure 2). The varying conditions particularly challenged the brightness adjustment part of the process. The method was also tested on 510 true-colour aerial images captured with the Microsoft UltraCam digital camera. Very-high-resolution satellite images are delivered in tiles. The area these tiles cover and the storage requirements depend on the sensor type. For the purpose of parallel processing, the tiles as delivered were rearranged into 1GB tiles. It is preferable to store images at different scales (pyramid levels) to speed up visualisation and the computation of image statistics at reduced images sizes. Each of the 1GB tiles forms separate inputs for the different CPUs.
Speed-up
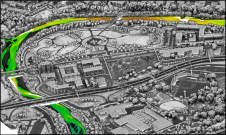
The total computation speed-up using parallel computing is a function of the computing time needed when using a single CPU, the computation time on multiple CPUs and a ratio that expresses the effects of the parts of the process that are not carried out in parallel (Figure 3). As experiments show that the nonparallel ratio of the process never exceeds 1% for large aerial and satellite tiles, computer clusters equipped with 100 to 200 CPUs will be efficient for mosaic production. In this test a computing cluster was used with 96 CPUs (Xeon E5-2695v2). On a single CPU computer the mosaicking of the 1m GSD satellite images took 60 hours while parallel processing on 96 CPUs took 50 just minutes, resulting in a speed-up factor of 72. Figure 4 shows the resulting orthomosaic. Mosaicking of the 510 aerial images required around 100 hours on a single CPU core and 101 minutes in parallel processing using the Xeon E5-2695v2 – a speed-up factor of 60. Hence parallel computing may speed up the creation of an orthomosaic from three to five days to around just one hour.
Parallel I/O
In the above-mentioned test, the reading and writing part (I/O) of the orthoimage creation process were conducted sequentially. However, parallelism can be employed not only in computing by expanding the number of CPUs but also in storing the data. RAIDs (Redundant Arrays of Independent Disks) make it possible to speed up reading and writing of files by combining various storage devices into one logical unit. How the data is distributed across the devices – usually hard disk drives (HDDs) – depends on (1) the level of redundancy required to avoid loss of data due to sector read errors or disk failures (reliability); (2) speed of reading and writing (performance); and (3) available capacity. An extension number from 0 onwards indicates the balance between these goals. Two principles underlie a RAID: stripping and mirroring. Stripping allows writing in parallel to a storage device by splitting huge amounts of data into smaller parts and pushing these parts to different HDDs simultaneously. Mirroring is storing the same data on several HDDs to improve reliability of data storage and also to speed up reading, as the data can be read from different HDDs simultaneously. Typical RAIDs have 300MB/s sequential access throughput and do not constrain CPU usage.
Random Access
The data needs to be transported from the RAIDs to the CPUs and back through a local area network (LAN). Therefore, the reading and writing times also depend on the LAN throughput. The I/O time is roughly linearly related to the array speed, i.e. a 300MB/s array is around three times faster than a 100MB/s array based on the same LAN speed. The authors’ experiments show, however, that a 600MB/s array connected to 4 GB/s LAN is only two times faster than a 300MB/s array connected to a 4 GB/s LAN. This is also true for a 100 MB/s array connected to a 2 GB/s LAN. This configuration is four times faster than a 20MB/s to 30MB/s array connected to a 1 GB/s LAN, although one would expect performance to be eight times better. Hence, the array and LAN speed alone do not tell the whole story. The reason is that some photogrammetric algorithms require random data access for which modern HDD-based RAID storage systems will give low throughput. Furthermore, the experiments show that using solid state drives (SDDs) instead of HDDs improves the reading performance even when only stripping is used.
Concluding Remarks
Photogrammetric algorithms can be effectively run on computer clusters with 100 to 200 CPUs. A fast data retrieval and storage system and high LAN throughput ensure the highest productivity.
Biography of the Author
Andrey Sechin graduated from Moscow Institute of Physics and Technology, Russia, in 1980 and obtained a PhD degree in mathematics in 1984. He is co-founder of Racurs, a photogrammetric company based in Moscow, where he has been scientific director since 1994. Before founding Racurs he was with Troitsk Institute for Innovation & Fusion Research.
Email: sechin@racurs.ru
Figure captions
Figure 1, Flow diagram of the orthomosaic creation process.
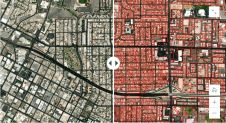
Figure 2, Block of around 200 GeoEye images on a background representing the DTM and detail (bottom).
Figure 3, Speed-up using multiple CPUs: T1 and Tp are computing time on one and p CPUs, respectively; a is a nonparallel ratio.
Figure 4, GeoEye orthomosaic – over 600 sheets have been produced at scale 1;10,000.
Value staying current with geomatics?
Stay on the map with our expertly curated newsletters.
We provide educational insights, industry updates, and inspiring stories to help you learn, grow, and reach your full potential in your field. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired.
Choose your newsletter(s)