Article

Dense Image Matching

Performance Analysis on Oblique Imagery

By Marianne Deuber, Stefan Cavegn, Stephan Nebiker • October 24, 2014

3D reconstruction using dense image matching is a hot topic as it enables the automatic extraction of 3D urban models, notably from airborne oblique imagery. However, applying DIM algorithms to oblique imagery is challenging because of large scale variations, illumination changes and the many occlusions. Here, the authors present a methodology for evaluating the performance of DIM algorithms and show the initial results from four DIM packages: Agisoft PhotoScan, Leica Xpro SGM, OpenCV StereoSGBM and SURE.

Dense image matching (DIM) aims at computing a depth value for each and every pixel of an image. This facilitates the generation of accurate and highly detailed digital surface models (DSMs). Until now, the studies performed on DIM have been mainly limited to nadir imagery, with only a few studies addressing oblique images. The methodology we have developed for the evaluation of DIM solutions applied to oblique imagery includes performance measures ranging from completeness and differences in image space to density and deviations from reference geometries in object space. Deviations to planes fitted through patches lead to an indicator for a single point cloud while deviations between the DIM output and reference points or profiles indicate performance of multiple point clouds, generally from different sources.

DIM Software

The four DIM solutions tested are mostly based on the semi-global matching (SGM) algorithm introduced by Hirschmüller (2008), and include:

- PhotoScan from Agisoft LLC implements a full photogrammetric processing chain based on computer vision algorithms

- Xpro SGM from Leica Geosystems, originally developed for DSM generation from ADS pushbroom data and later adopted to frame sensors, is not yet fully optimised for oblique images

- StereoSGBM from the open source library OpenCV consists of a simplified variant of the SGM algorithm and is limited to a radiometric resolution of 8 bit

- SURE from the University of Stuttgart and now distributed by its spin-off nFrames.

The workflow to arrive from stereo images to a DSM can be subdivided into five stages: (1) image rectification; (2) image matching and depth map extraction; (3) point cloud generation; (4) DSM computation; and (5) DSM texturing. The two DIM packages Agisoft PhotoScan and SURE perform all these tasks and are therefore the most complete with respect to workflow (Table 1).

Task	Photo-Scan	Stereo-SGBM	SURE	Xpro SGM
image rectification	V		V
image matching	V	V	V	V
point cloud generation	V		V	V
DSM computation	V		V
DSM texturing	V		V

Table 1, Tasks performed by the four packages tested.

Site and Data

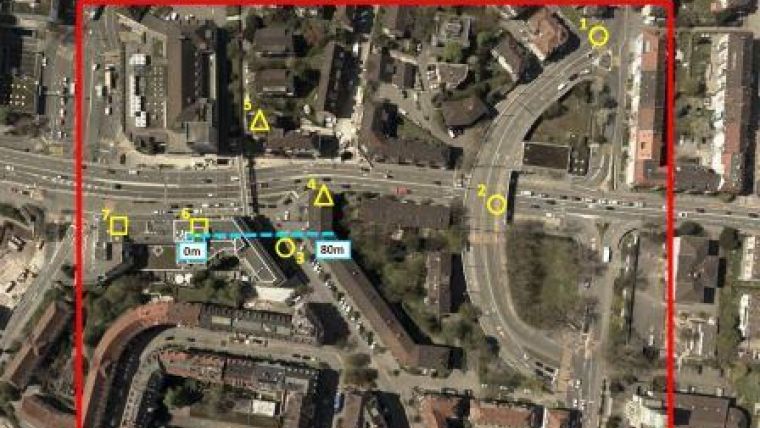
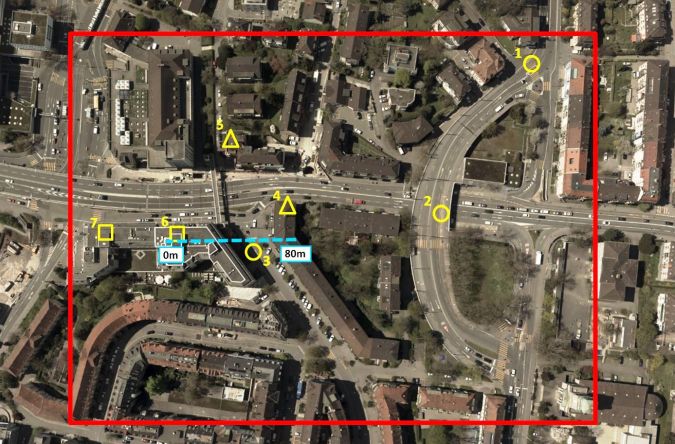
The test area covers 5 hectares of Zürich West (Figure 1). The urban area has been recorded with a Leica RCD30 Oblique Penta which consists of five camera heads, one looking nadir and the others looking forward, backward, to the right and to the left with a tilt angle of 35 degrees. Each head has a sensor size of 60MP with a pixel size of 6 micron and a radiometric resolution of 14 bit. Images were captured with a nadir overlap of 70%/50% at a flying height of 520m. With a focal length of 53mm the ground sampling distance (GSD) of the nadir images is 6cm and the GSD of the oblique images ranges from 6cm to 13cm. Prior to matching, the images were precisely georeferenced. Reference data includes point clouds from terrestrial laser scanning (TLS) and a DSM derived from Leica ADS100 data.

Figure 1, Test area (red), location of reference patches for scatter evaluation (yellow) and profile (blue) depicted in Figure 5.

Completeness and Depth Differences

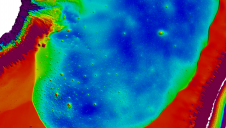
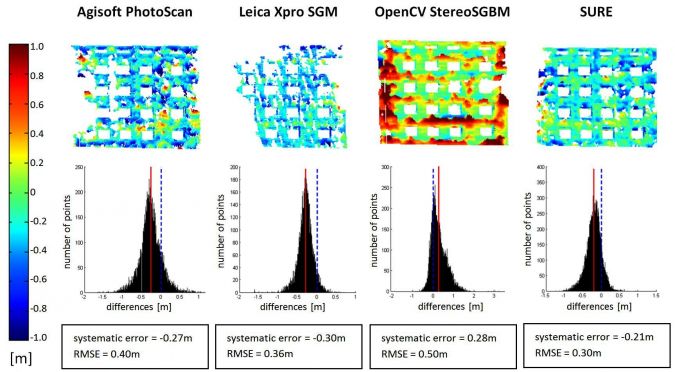
Completeness is the ratio between the number of pixels to which the software assigns a depth value and the total number of pixels. Areas covered by vegetation and shadows were particularly challenging. For the whole test area, SURE shows the highest completeness with 78%, and with 60% Leica Xpro SGM shows the lowest. Figure 2 illustrates the spatial distribution of the points for which a match was found for a 0.5ha cropping of the test area. Although the depth map of Xpro SGM shows fewer holes than that of PhotoScan or StereoSGBM, the percentage is lower as the point density in the matched areas for Xpro SGM is generally lower. Figure 3 depicts – in the form of maps, histograms and values – the depth differences for building façades generated from left-view DIM and TLS points. The systematic errors range from 21 to 30cm and the root mean square errors (RMSEs) reach up to 50cm. SURE shows the best results.

Scatter and Density

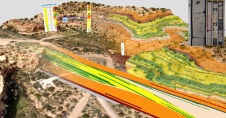
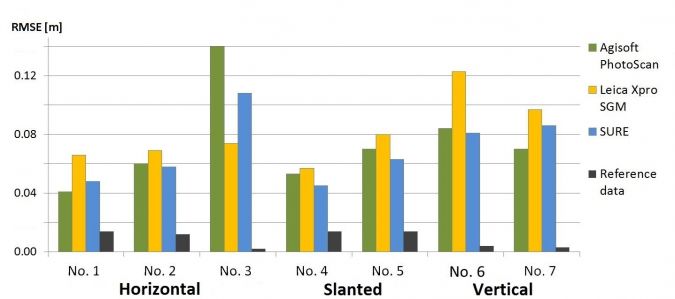
Scatter can be computed by fitting a plane through a point cloud subset and by determining the RMSE between the points and the fitted plane. Here horizontal, slanted and vertical areas of about 10 m² were selected as depicted in Figure 1, and the RMSE was computed for both DIM points and reference points captured by an ADS100 sensor and TLS respectively. For the forward view, street (horizontal) and roof (slanted) patches with the exception of shadow areas showed an RMSE of about 1 GSD (Figure 4). Larger RMSEs of 1-2 GSD were obtained for façades, i.e. vertical areas. The other oblique views yielded similar results. A further measure is point cloud density which is defined as projected points onto a plane per square metre.

Profiles and Points

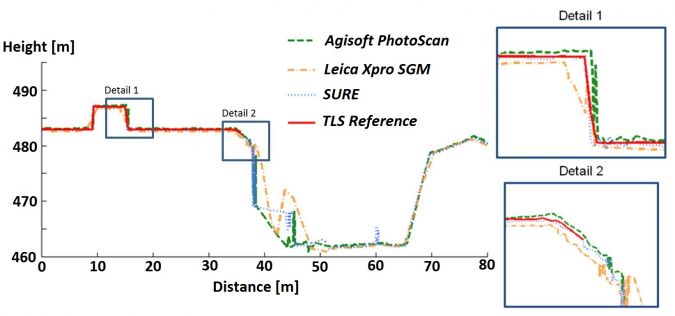
Reference profiles are a proven method for analysing matching resolution, potential systematic errors and accuracy. Figure 5 shows that profiles of roof details captured by TLS and DIM profiles from oblique views correspond well. Larger differences occur in regions of building shadows (around profile position 40m). Comparing the 3D coordinates of distinct points is challenging because reference data should be homologous with points, lines and shapes generated from point clouds. Therefore, three adjoining planes such as roof parts were fitted through the respective point cloud and intersected. To obtain reliable results, scatter should be low and the number of points per plane sufficient. Table 2 shows accuracies of absolute coordinate differences of homologous points. On average, coordinate differences of 12 points per matcher and viewing direction were incorporated in the accuracy computation. The RMSEs for 3D point coordinates were 1 to 1.5 GSD horizontally and vertically, with a maximum of approximately 2 GSD.

Table 2, Accuracy of absolute 3D coordinate differences (RMSEs) for homologous points.

Concluding Remarks

Absolute point accuracies are about 1 GSD horizontally and vertically for nadir and oblique imagery with camera heads facing across the flying direction, and 1 to 2 GSD for forward and backward oblique viewings. The methods for evaluating and comparing DIM performance have proven to be efficient and practical for different image matchers, for diverse oblique viewing geometries and for complex urban scenes, including building façades and other vertical structures. Parts of the methodology will be used in the upcoming ISPRS benchmark on high-density image matching for DSM computation.

Acknowledgements

Thanks are due to Leica Geosystems AG (Heerbrugg, Switzerland) for providing the accurately georeferenced oblique imagery and a reference DSM.

Figure 3, Depth differences between DIM and reference points represented as maps (top), histograms (middle) as well as systematic and RMS errors.

Figure 4, RMSE of different planar patches for forward-looking imagery.

Figure 5, Profiles of roofs and a street derived from two forward images.

Value staying current with geomatics?

Stay on the map with our expertly curated newsletters.

We provide educational insights, industry updates, and inspiring stories to help you learn, grow, and reach your full potential in your field. Don't miss out - subscribe today and ensure you're always informed, educated, and inspired.

Choose your newsletter(s)