Official Geoid Undulations Model

The classical geodesist’ dream of a dense, accurate, reliable and homogeneous countrywide levelling control network is a luxury even for the richest countries and will probably remain a dream. Prior to the GPS era there was no alternative to precise levelling. Now there is. The authors suggest a new approach to orthometric height control in which the best available geoid model is used as official, statutory model from which to deduce countrywide orthometric heights, while ellipsoidal heights are measured with GNSS. Developing countries may benefit. A geoid model is prerequisite for deriving orthometric heights from GNSS measurements. But is it really necessary to determine a true geoid model with centimetre accuracy to obtain orthometric heights at centimetre accuracy This question is opportune since all around the world enormous efforts are being made to achieve high-accuracy geoid models. We challenge the need for this: any geoid model suffices to achieve the accuracy required for most engineering works. It is not necessary to strive for the perfect model. The only requirement is that the geoid model for a certain region be consistently applied and officially approved. We call such an official, statutory model the Official Geoid Undulations Model (OGUM).

Inconsistencies
Classical vertical control consists of hierarchical networks following the principle ‘from the whole to the part’. The primary network is obtained by precise levelling and the loops are some hundreds of kilometres in length, while accuracy should be at mm/km level. The lower networks represent densification of the primary network, with decreasing accur–acy according to needs. Establishment of a third-order network is only feasible in densely populated areas and it is difficult to get heights for lower-order networks with absolute accuracy (relative to the higher-order) better than 5-10cm; such discrepancies are found between neighbouring municipalities. Inconsistencies in the heights of lower-order control points are inevitable as long as these points are separate and not part of a dense, well-maintained network of, say, less than 2x2km.

GNSS
Ellipsoidal control is the imminent replacement for orthometric control. Vertical ellipsoidal (geometric) control should be based on a permanent GNSS network that constitutes the first order of 3D control. Operating costs mean permanent stations lying tens of kilometres apart. Since GNSS accuracy depends on the length of baselines and these are compensated for by longer measuring sessions, especially in the vertical direction, densification is recommended for the first-order control according to needs. This should, of course, be accomplished by GNSS measurements. In Israel the accuracy of the second-order network will be 1cm (2.), and that of the third-order 2cm, relative to nominal heights of permanent GNSS stations.

Geoid Models
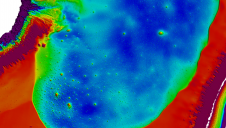
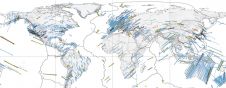
Geoid models constitute an import–ant part of modern geodetic infrastructure and enable conversion of ellipsoidal to orthometric heights. Intensive use of GNSS for geodetic and engineering applications necessitates the fast development of a geoid model of which basically two types are currently in existence (Figure 1). Firstly, there are geopotential models based on gravity measurements the accuracy of which depends on density of such measurements, accuracy of DTM, assumptions made of mean specific weight of soil etc. Secondly, geometric models based on ellipsoidal heights of benchmarks obtained by GNSS measurements, accuracy depending on point density and accuracy of ellipsoidal and orthometric heights. Integration improves the geoid models. To deduce national orthometric heights that will ‘live in peace’ with the heights of the benchmarks from a geopotential model some biases between the two systems have to be eliminated.

Substitute
Endless efforts seem to be being made to improve the geoid model to achieve 1cm-level accuracy everywhere in a country, just like the efforts to achieve a levelling network of this kind. A national vertical control network has to bring consistent and identical heights to all points within the desired accuracy obtained by every surveyor. This goal is practically impossible using classical levelling networks. It is also impossible if we have to wait for completion of a geoid model accurate everywhere. To overcome this problem we suggest declaring the best available model Official Model for a certain time, to be replaced periodically by an improved model. Documentation for each version should be maintained and applied whenever a change of datum is required. The combination of OGUM with vertical ellipsoidal control based on Continuously Operating Reference Stations (CORS) produces a practical countrywide network of orthometric height control appropriate for most geodetic/surveying needs. Our idea is not a ‘magic panacea’ for everything everywhere; its use depends on the specific needs for accuracy of orthometric height, accuracy of vertical ellipsoidal control network and accuracy of the best-available model. Projects re–quir–ing higher accuracy do not need a nationwide accurate ortho–metric control system, since use can be made of local ‘orthometric islands’ of higher accuracy. A certain benchmark the orthometric height of which has been deduced using this technique may obviously determine the datum for a local orthometric island.

Experiments
The accuracy required is rarely better than 1cm in orthometric height difference between two points 100 metres apart; that is a relative accuracy of 100ppm. However, an accuracy of 10cm between two control points 1km apart is not satisfactory. This is due to the nature of levelling, where one may make a gross error of 10cm but still not find any abnormal misclosure having conducted one-way levelling. Thus for orthometric control of fourth-order, accuracy is needed of about 25mm between benchmarks 1km apart; that is 25ppm. To verify our suggestion and to estimate the accuracy of the orthometric height differences we conducted experiments in Israel using the worldwide geopotential model GPM98B and an Israeli geo–metric geoid model. All experiments with the temporary Israeli OGUM achieved relative accuracy better than 25ppm (Figure 2) and the same was true for the GPM98B model, except for Eilat (one of ten locations), probably due to the rugged topography of this area. These results demonstrate the capability of our idea for most engineering works. It is especially adequate for orthometric control points for large-scale topographic mapping.

For Rich and Poor
This approach should not be used where a dense and stable levelling network of accurate and consistent control points already exists. But developing countries may benefit because establishing a classical network is ‘mission impossible’ here. As professional surveyors it is our duty to understand the applicability of the OGUM to our needs. The main issue is the accuracy of the model, and the best available model should be chosen. A nationwide model requires a best fit with the benchmarks, affirmed by direct GNSS measurements at certain of them. A global model can be used when nothing better is available, but then it should be fitted to as many benchmarks as possible. We found differences of up to plus (in the north) and minus (in the south) 1.9 metres between the Israeli model and the GPM98B over a distance of about 400km. As the general rules of geodesy mandate, it is important to know the accuracy of the chosen model and to use it accordingly.

Concluding Remarks
OGUM is an appropriate substitute for the national levelling network, and users can gain greatly from it. But they should also be aware of its limitations and that a nationwide orthometric island is created. The big advantage is consistency and its being ‘errorless’; nominal accuracy of orthometric height at a point depends on the accuracy of the GNSS measurements alone. We hope that the idea will help those countries that cannot afford the luxury of establishing and maintaining dense levelling networks, and this may even be the case in most developed countries.

Further Reading
• Sharni D., and Papo H., 2000, The Carmel Mountains Precise Geoid. ‘Quo Vadis - International Conference’, FIG Working Week 2000, 21-26 May, Prague.
• Steinberg G., and Even-Tzur G., 2006, ‘Permanent GNSS Networks and Official Geoid Undulations Model as a Substitute for Orthometric Control’. XXIII International FIG Congress, 8-13 October 2006, Munich, Germany.
• Steinberg G., 2006, New Survey Regulations for Israel. XXIII International FIG Congress, 8-13 October 2006, Munich, Germany.
• Steinberg G., and Papo H., 1996, Vertical Geodetic Control of the
Future. Geoinformatics ’96, Wuhan International Symposium, Wuhan, China.
• Wenzel, H.G., 1998, Ultra-high degree geopotential models GPM98A, B, and C to degree 1800. Proceedings of the Joint Meeting of the International Gravity Commission and International Geoid Commission, September 7-12, Trieste, Italy.