Deep learning for ground and non-ground surface separation

As a division of machine learning, deep learning (DL) has been achieving unparalleled success in image processing and recently demonstrated huge potential for point cloud analysis.

Precise ground surface topography is crucial for 3D city analysis, digital terrain modelling, natural disaster monitoring, high-density map generation and autonomous navigation, to name but a few. Deep learning (DL), a division of machine learning (ML), has been achieving unparalleled success in image processing, and recently demonstrated huge potential for point cloud analysis. This article presents a feature-based DL algorithm that classifies ground and non-ground points in aerial laser scanning point clouds.

Recent advancements of remote sensing technologies make it possible to digitize the real world in a near-automated fashion. Lidar-based point clouds are a type of remotely sensed georeferenced data, providing detailed 3D information on objects and the environment, and have been recognized as one of the most powerful means of digitization. Unlike imagery, point clouds are unstructured, sparse and of irregular data format. This creates many challenges, but also provides huge opportunities for capturing geometric details of scanned surfaces with millimetre accuracy. Classifying and separating non-ground points from ground points greatly reduces data volumes for consecutive analysis of either ground or non-ground surfaces, which consequently saves costs and labour, and simplifies further analysis.

Machine learning and deep learning

Machine learning methods with a long history of automatic classification include well-known methods such as Support Vector Machines and Random Forest. However, they are often criticized for their limited generalization capability due to the use of shallow architectures. On the contrary, artificial neural networks with several hidden (internal) layers use a so-called deep architecture which has been applied in recent years with unprecedented success. The main challenge of implementing a supervised DL method is that it requires a sufficient amount of labelled training and validation data to tune a successful classification model. Many researchers believe that the end-to-end DL approach can extract useful features automatically from raw data, and therefore no feature engineering is required, but this is not always true. This article argues that the use of appropriate features can solve classification problems more efficiently while using fewer resources, i.e. a small number of layers and less training data. However, implementing a feature-based DL method needs a clear understanding of both problem and data structure to extract powerful features. The architecture presented in this article, which was originally proposed in the paper by Nurunnabi et al. (2021), is a feature-based DL classification approach that labels ground and non-ground points in airborne laser scanning (ALS) point clouds.

Feature extraction

The proposed algorithm consists of two steps. The first step performs feature design and extraction, while the second step develops the DL architecture (Figure 1). Based on an extensive review of state-of-the-art literature, the authors selected the most promising and successful features used for defining the characteristics of points based on their local neighbours. Features are derived using spherical and cylindrical neighbourhoods of each point of the data. A spherical neighbourhood with a user-defined radius is used to obtain 3D geometric features (GFs) based on the covariance matrix generated by the coordinates of the neighbour points (x, y, z). Principal component (PC) analysis is performed to estimate eigenvalues and eigenvectors from the covariance matrix that are used to derive the necessary features. The most common 3D GFs, also known as covariance features (CovFs), are: point normal, curvature, first PC, three eigenvalues, linearity, planarity, scattering, omnivariance, eigentropy, plan offset and verticality. Vertical infinite cylindrical neighbourhood (with the same radius as the spherical neighbourhood) is used to obtain cylindrical features that relate to the heights of the points (z values). These are the minimum, range, mean, and variance values of z, and the relative position of the point of interest  within its neighbourhood. Additionally, point density, return number, intensity, positive openness and echo ratio are used.

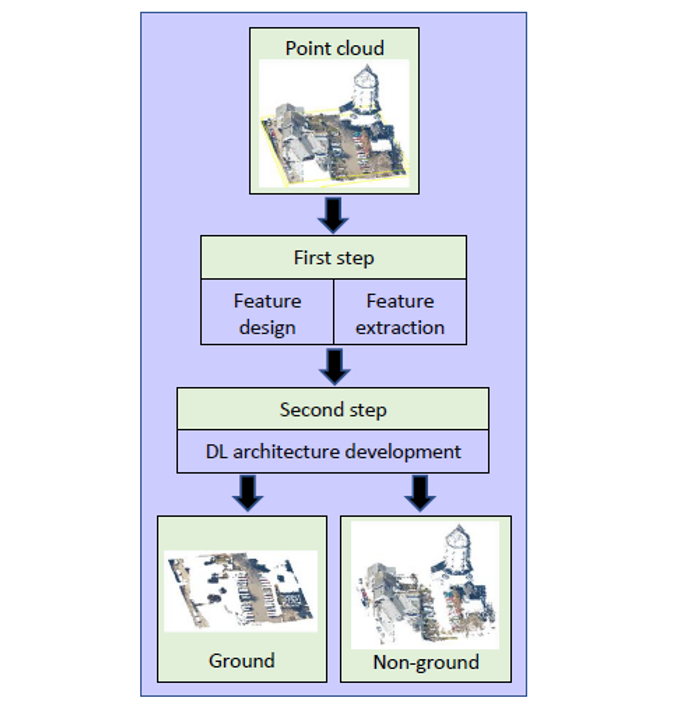
Deep learning architecture

The proposed architecture develops a binary classifier and follows a straightforward artificial neural network (NN) workflow. The inputs for the network are the feature vectors, and the outputs are the labels of ground (1) or non-ground (0). Fully connected network layers are used with a rectified linear unit (ReLU) activation function for the hidden layers, and a Sigmoid function is used for the output layer. Binary cross entropy is used as loss function, while the use of an Adam optimizer speeds up the model training process. A so-called He initialization strategy and Batch normalization are used to reduce the influence of vanishing and exploding gradients. Evaluation of the model is needed to fine-tune the necessary hyper-parameters. The network consists of five hidden layers with 50 neurons per layer. Inputs are processed with a mini-batch size of 128. The network is trained with 50 epochs and the one that achieves the highest accuracy is selected as the final model. L2 regularization with a learning rate of  is used to avoid overfitting. The relevance of the features is studied in several groups (Models) to identify the optimum ones producing the best results.

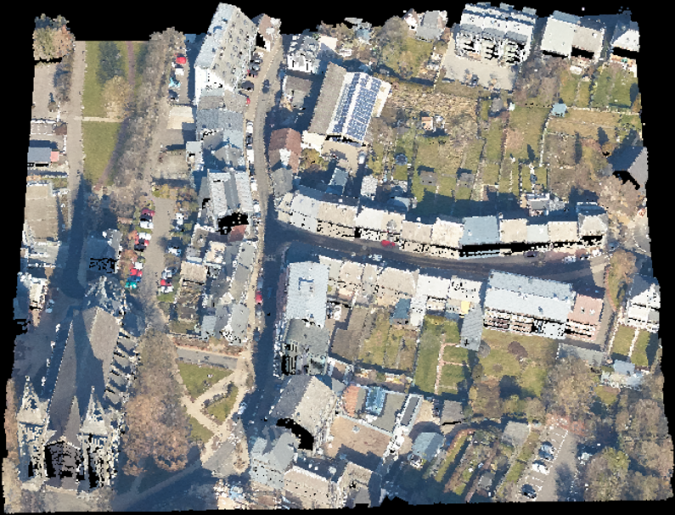
Open-access airborne Lidar dataset

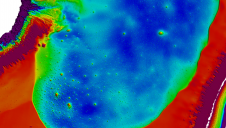
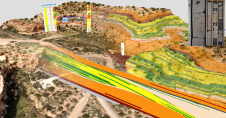
The newly developed algorithm can be demonstrated based on an open-access airborne Lidar dataset provided by the Administration du Cadastre et de la Topographie (ACT) of Luxembourg. Average point density, horizontal and vertical precision of the data are 15/m², ±3cm and ±6cm, respectively. The data is organized into 500m 500m tiles, each of which contains on average 5-7 million points. The points are labelled into classes, e.g. soil, vegetation, buildings, water, bridges, power lines and unclassified. Additional manual editing was performed to obtain more accurately classified data as ground and non-ground points (Figure 3). Two tiles from a semi-urban area (Dudelange, Luxembourg) were selected for use with the algorithm. The test dataset has a height difference of around 20m between the highest and the lowest points.

Demonstrating the algorithm

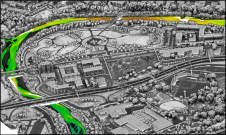
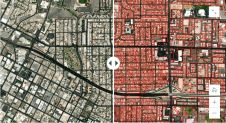
From the selected tiles, one tile was used for training and validation, while part of the other tile was selected as test data (Fig. 2). The training-validation tile was sliced into five segments, and one of them was randomly selected as the validation set. The training, validation and test sets consist of 3,481,758 points, 650,764 points and 970,387 points, respectively. The required input vectors were generated with a neighbourhood size of 100cm radius and the proposed algorithm was applied using different combinations of features. Model 3 was identified as the best group of features as it achieves the highest accuracy among the three considered models. It consists of a set of 17 feature vectors: point normal, curvature, linearity, planarity, scattering, omnivariance, eigentropy, plane offset, verticality, point height z, range-z, mean-z, variance-z, point density, positive openness, echo ratio and intensity. Model 3 achieved the highest precision of 99.77% for ground surface extraction, an F₁ score of 97.5% and 97.8% for labelling ground and non-ground points respectively, and an overall model accuracy of 97.7% (Figure 4).

Separating ground from non-ground points

The algorithm for pointwise classification (also known as semantic segmentation) of point clouds used three models which are three different combinations of extracted pointwise local features. The inputs for the networks are point features, rather than the raw point coordinates (x, y, z). It can be concluded that accurate estimation of the height values of the points has significant impact on results.

The discussed approach could be successful as a so-called work-horse method to efficiently separate ground from non-ground points. It combines a high accuracy with relatively low computational load. This distinguishes this method from recent end-to-end deep learning point cloud methods, which typically require heavy and extensive training and are therefore more difficult to perform on a standard desktop computer. The non-end-to-end approach described here accepts more information-rich input (i.e. the feature vectors) and therefore requires fewer internal layers. As a consequence, fewer parameters (i.e. the weights of the neuron connections) have to be determined, which makes the method much lighter and more efficient.

Concluding remarks

The proposed feature-based DL algorithm classifies ground and non-ground points in ALS point clouds with a high rate of accuracy. It presents a fully connected deep neural network approach to develop a binary classifier. The authors showed in the original paper that, unlike most feature-based algorithms, the new algorithm does not require multi-scale neighbourhoods. Hence, it can reduce a significant amount of the computational complexity and saves time when compared to many existing feature-based algorithms. The new classification algorithm is simple but efficient to perform. This is because the architecture is shallow but powerful, which reduces the computational burden, and extracts both ground and non-ground points efficiently in the presence of steep slopes, non-smooth terrain and with significant height variability. However, the proposed feature-based DL algorithm requires a thorough understanding of both the saliency features used as input vectors, and the data properties for tuning the hyper-parameters in the model-building process in order to achieve the highest classification accuracy.

Acknowledgements

This work is supported by the Project 2019-05-030-24, SOLSTICE – Programme Fonds Européen de Developpment Régional (FEDER)/Ministère de l’Economie of the GD of Luxembourg.

Further Reading

ACT/Dudelange data: https://data.public.lu/en/datasets/lidar-2019-releve-3d-du-territoire-luxembourgeois/

LeCun, Y., Bengio, Y., Hinton, G., 2015. Deep learning. Nature, 521(7553): 436-444.

Nurunnabi, A., Teferle, F. N., Li, J., Lindenbergh, R. C., Hunegnaw, A., 2021. An efficient deep learning approach for ground point filtering in aerial laser scanning point clouds. The Int. Arch. of the Photogramm. Remote Sens. Spat. Inf. Sci., XLIII-B1-2021, 31-38.